依托学生的思维起航
——特级教师贲友林“找规律”教学片段赏析
当数学知识的学习,让学生觉得不再繁难时,我们说,我们的课堂就成功了。特级教师贲友林,以睿智而大气的课堂,带着大家一起思考、实践,永不停歇,寻找课堂中的快乐,执教的苏教版四年级上册《间隔排列》一课,演绎出了一位具有“哲学思想内涵”教师的风采,娓娓听来,总是那么让人受益匪浅。
【片段一】引领——见力度
新课伊始,请一名学生上黑板完成听写活动,依次画圆、三角形(3个圆和3个三角形)。
师:是圆多还是三角形多?
生:(齐答)同样多。
师:如果继续画,你知道画什么吗?
生:圆,三角形……
师:你怎么知道的?
生:它们是有规律的。
师:圆和三角形的排列是有规律的。(板书:规律)仅注意规律我还不太满意,告诉大家圆和三角形的排列有怎样的规律?
生:一个圆一个三角,
师:好的,我们现在换一个角度看,两个圆之间夹一个三角形,两个三角形之间又隔了一个圆,像这样圆和三角形的排列方式我们又可以说是圆和三角形是“间隔排列”。(板书:间隔排列)接下去会不会画?继续。
【赏析】
新课一开始,贲老师就组织听写活动,先由教师说,学生完成画,继而让学生自己依循着自己的认识尝试画,看似简单的环节,却是“曲调未成心先动”,素朴的活动,轻轻推开了学生的思维之窗,“规律”之痕已在不经意间印烙在学生的心间。没有奢华的言语,却在一个小小的序曲活动中效达成了两个目标:一是完成了对规律认识的起步,孕伏了“规律本无形,只需用心悟”的思想,凸显了“找”规律这个核心要领,暗指了规律要“找”的质朴方法,这也是追寻数学课堂本质回归的应然诉求;二是达成了学生经验知识向数学知识的序列转化与递进,并以此为引线,为后续的学习做好了坚实的铺垫,逐步向纵深推进。
【片段二】体悟——求精度
师:如果我不说停,你们准备一直画下去?画呀!
(大家笑着不言,板演学生已经画到黑板边缘,画无可画。)
生:画个省略号。
师:早就该想到这个办法了!(擦除多余,写上省略号)规律一切尽在不言中。
(结束活动。黑板上留下:○△○△○△……最后,教师再在后面补上一个圆和三角形,出现:○△○△○△……○△)
师:圆有多少个?你能数得出来吗?
生:不能。
师:三角形呢?
生:不能,都有无数个。
师:圆和三角形谁多呢?
生(齐声答):一样多。
师:有意思,我都数不出来,还怎么说它一样多呢?
生:因为开头是一个圆一个三角,前面部分一样多,最后还是一个圆一个三角,所以他们一样多。
师:听你这么讲我还觉得不过瘾,到前面指着图讲。可以用红粉笔做做标记,让大家能听懂、看懂你的想法。
生:前面是一个圆一个三角形,后面还是一个圆一个三角形,如果最后还是一个圆,那就是圆多,但是后面还有一个三家形,所以一样多。(并在开头的圆和三角形下面有红色小圆做了标记)
师:听明白了吗?你觉得她是怎么比较的?
生:她是根据前面的已知情况来判断后面的情况的。
师:是呀,看,这还有标记,我把这两个标记连接起来,你看行吗?
○△○△○△……○△
师:(指着连接起来的一组)再这里面有几个圆,几个三角形?哦!有一个圆就有一个三角形,有一个三角形就有一个圆。
(下面连接后面的每组圆和三角形,发现都是一个圆对应一个三角形)
师;其实,在这里面呀,圆和三角形是一一对应的,(板书:一一对应)所以现在我一看就知道了,圆的个数和三角形的个数是相等的。非常好,现在,我再画一个圆。
生:那就是圆多了。
师:多多少呢?
生:圆比三角多1个。
师:为什么呢?
生:因为他们前面都是一一对应的,相等,后面又多出一个圆,所以圆比三角形多一个。
师:最后一个圆没有对应的三角形。
【赏析】
心理学认为:“只有经常性启发学生动手、动口、动脑,自己去发现问题,解决问题,才能使学生始终处于一种积极探索知识,寻求答案的最佳学习状态中。”
听写活动已经演变成了“自主接力画”,当然,这是学生基于对“规律”的自我解读之上进行的,这时他们对“规律”的认识还是浅表的、不甚清晰的。在“画不下了”、“画无止境”的现实矛盾中,首先想到了“用省略号”,这是对规律由显性向隐性转变的开始,贲老师借机介入,顺应着学生的思考,思、辨、研、磨,让学生用朴素的、基于自己原生态认识的语言,理解“一一对应”的关系,并以此为“支点”,厘清规律的内涵,悟透规律的本质。
以组织活动、线性行进的形式,相机揭示规律,已经跳出了教材固有的教学流程,也基本颠覆了以往教学“间隔排列”基本要素的呈现,“两端物体”、“中间物体”、“封闭图形”只字未提,不难看出,贲老师在几番思量之下的双“重”体现。
尊重学生个性经验的释放,淡化学生对语言的表达要求,让学生“用自己的话”来阐述规律,如:“一个圆接一个三角形”,“用前面的已知情况来判断”等,不一而足,无甚修饰,却也言之凿凿。
注重规律本质内涵的追求,以活动为载体,以解决和深化为目标,紧攥“一一对应”这一本质要点:如果两种物体都能一一对应找到“朋友”,即两种物体的个数是相等的,如果两种物体不能“一一对应”,则最后没找到对应“朋友”的物体多1。浅显而又平实,却正是“间隔排列”最有力的注释。
【片段三】处理——见深度。
把书本上的例题情景呈现,寻找间隔排列现象,由学生上台做介绍,说思路,理关系,强化“一一对应”的内涵,悟透规律。

师:好,我们继续看图,(隐掉夹子和手帕,分别以圆和三角替代夹子和手帕)这里圆表示什么?三角形呢?
(用线成组连接○△○△○△○△○△○△○△○△○△○)
师:是呀,一看就明白了,前面一一对应,最后一个圆没有对应的三角形,所以夹子比手帕……
生(齐接):多1。
(依次把兔子和蘑菇,柱子和网用圆和三角替换,说说认识。)
师:真好,那咱们可以吧三幅图合并成一幅图,这里用圆表示夹子、兔子、柱子,用三角形表示手帕、蘑菇、网。
(先动态合并出一个圆和一个三角形,然后成组合并出现,最后各个图上最后一个圆依旧单独留着,呈:○△○△○△……○△)
师:圆表示的物体和三角形表示的物体它们的个数有什么关系?
生:一一对应。
师生同说:它们是一一对应的,所以它们个数是相等的。
师:好的,如果最后还有一个圆表示物体,那么这时圆的的物体比三角形的物体怎么样?
(合并后如图:○△○△○△……○△○)
生(齐):多1个。
师:这个图好像在哪见过?哦!前面我们研究过,现在我们再看这幅图,想法一样吗?现在在这里圆表示一种物体,三角形呢?表示另一种物体,这两种物体的间隔排列,现在我们继续看图。(隐去所有三角形)
师:哦,只剩下一种物体了,不过,这物体和物体之间出现了空的间隔,物体的个数和中间的间隔数有什么关系。
生:物体的数量减1等于间隔数。
师:也就是说物体的数量比间隔怎样?(多1)为什么呢?
生:因为物体的最后一个圆没有对应的间隔。
师:她说最后一个物体没有对应的间隔,所以想到什么?
生(齐):物体比间隔多1。
师:谢谢!(齐鼓掌)在生活中有没有这样间隔排列的物体呢?
……
【赏析】
爱因斯坦说:“我思考思考问题时,不是用语言进行思考的,而是用活跃的、跳跃的形象进行思考(用形象思维思考问题),当这种思考完成之后,我要花很大力气把它转换成语言(由形象到抽象思维)。”
依据以上认识,贲老师依托书本的主题情境图(例题),再次完成对规律的强化认识。如果说,之前的由学生听写绘画,自主尝试绘画,到这里的例题情境中规律的再认识,是对规律形象化的直观认识,那么之后,借助主题情境图进行灵动、精致的处理(隐去情境图形,用三角形和圆形来替换),可谓是匠心独运,既与前面所学知识进行了贯通,又拓展了新知,向更为高的层析进行迈进。由特殊到一般的过程,用“符号化的思想”,将新知识纳入到自己适当的认知结构中去,能依据自己已有的知识和经验,对新知识作出自己的解释,用自己的语言对其重现编码,对新知识与自己原有认知结构的适当性作出自己的评价和调整,并在两者之间建立联系,从而使新知识在心理上获得确定的意义。形象思维向抽象思维的跨越,图像化向符号化的过渡,自然无痕,处理精当。
贲老师深厚的处理功力,在此显露无遗。其深度的把握,一方面来源于对教材个性化的理解和创造性的解读,另一方面则是基于对学生思维航向有效的调控和洞悉,以动态的、发展的眼光去发现、剖析静态知识的演变过程及规律的形成过程,达成“规律的认识由模糊变得清晰、从浅表转向深刻、从零散形成整体,真正实现为学生的理解而教。
【片段四】练习——显效度。
音乐《找朋友》响起
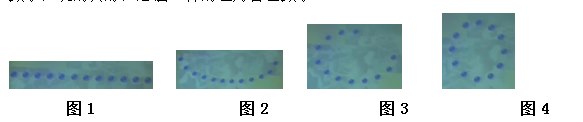
师:你现在看到的是根据《找朋友》这首歌编的一个舞蹈,这是一个舞蹈的示意图,12个圆表示12个男生。如果在男生之间插入女生,12 个男生能插入多少个女生?(见图1)
生:齐:11个,
师:每个男生都能找到一个对应的女生做好朋友嘛?
生:不能!最后一个找不到好朋友
(队形变化,见图2)
师:12个男生,能插入多少个女生?依旧是11个。
(队形变化,见图3)
生:还是11个。
(队形变化,见图4)
生:12个。
师:怎么回事?(停顿一会之后),怎么前面都是12个男生,11个女生,这里怎么有的同学说12个男生12个女生了?同桌两个人先交流一下!
生(上黑板展示,大家掌声鼓励):因为最后一个男生和第一个男生之间又出来一个间隔,所以还能插进去一个女生,所以男生和女生就是一样的个数了。
师:谢谢,在这个之前,12个男生,11个女生,正如刚才的同学说,
生(齐接):第一个男生和最后一个男生又产生了一个间隔,所以还能插入一个女生。
师:所以12个间隔能排12个女生,真好,谢谢大家。看!有人点头有人鼓掌,说的真好,想法一样的也为自己鼓掌。
【赏析】
在这一环节中,贲老师是力求间隔排列的规律由“非封闭图形”向封闭图形的突破,他没有采用书本现成的习题,而是以编舞排队这学生喜闻乐见的形式展开。贲老师通过“找朋友”舞蹈的队形变化,用了四个层次,在学生经历由“非封闭图形”到“封闭图形”的变化中,领悟封闭图形间隔排列内在规律的特质。在这里,贲老师用动态渐变的方式,四次调整队形,由直线排列转为圆形封闭排列,避免了学生思维由于过渡跳跃而带来的中断,拓展升华,把课堂的气氛推向了高潮。
习题承载着多重教学目标,有效、高效的引领,要用多重视角剖析静态习题蕴涵的数学价值,动态处理,由一个点铺展到一个面,让学生在解题的过程中积累数学活动经验,掌握解题策略,感悟数学思想方法,适度的升华,其效果也必然卓著。贲老师对习题实施了动态层面上的再加工,注重凸显学生在练习活动中情趣与理趣的追寻,带来的不光是视觉冲击,对知识与技能、情感态度与价值观的的习得与形成,基本素养的渗透也是绵延不尽的,可说是学与用同构,情与智共生。
力度、精度、深度、效度的奋力追求与演绎,精彩得以彰显。在贲老师的整堂课中,承顺着学生的思维,对规律的“找”与“悟”,是贯穿课堂的主线。课堂中,没有强制的灌输和机械的套用,基于学生原生态的认识使真实有效的数学活动直接指向数学的本质,并且不断地将学生的认知推向深入,细细回味,余香袅袅,时时散发出迷人的智慧光芒。
《江西教育》2015年3期

 苏公网安备 32041202001123号
苏公网安备 32041202001123号 