作为一名数学教师,每天都希冀孩子们在自己的授教下,能长知益智,收获成长的喜悦,但不可避免的是,面对一些教学内容,直视面学生习题中的各色错误,我们无时无刻不在煎熬中反思:到底该怎么教,孩子们才能融会贯通,并做到举一反三?众人之困,亦是我之所惑。
是我们不会教了吗?显然,答案是否定的。每一位教育者,都是从孩提时代走过来的,也会不断地以孩子的视角去审视当下的教学内容,当初我是怎么想的,又是怎么学的?我也在这样的苦恼中,一路追问,一路探寻。直至,一道习题的出现,让我从孩子身上受教,原来,成人化的思维,蒙蔽了我们教学的“眼睛”,俯视成了我们一贯的动作,而少了该有的平视、仰视——蹲下身、擦亮眼去洞察孩子们的想法。
【案例】
在学习完了“长方形和正方形”这一单元的内容后(苏教版小学数学三年级上册),出现了如下一道习题:
把一个边长是20厘米的正方形硬纸板剪成4个大小相同的小正方形,每个小正方形的周长是多少厘米?(如下图)
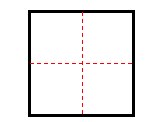
在批阅时,有近一半的学生的答案是:20×4=80(厘米),80÷4=20(厘米)。
孩子们的解法,到底是出于何种想法,带着心中的疑虑,我进入了课堂,与学生进行了正面“交锋”。在抛出如上解法之后,我与孩子们的思维“对垒”就此展开。
探问:为什么这样算?
师:孩子们,你为什么这样算的呢?
生1:20×4=80(厘米),这是先算出大正方形的周长,因为需要求出每个小正方形的周长,这里正好分成了4个相同的小正方形,所以,把大正方形的周长除以4,也就是用80÷4,就可以算出每个小正方形的周长了。
(众多学生点头示意,表示赞同 。)
【旁白:原来如此,回答得直接干脆,我内心却豁然开朗,求出大正方形的周长,再平均分一分,孩子们有错吗?扪心自问,在以往的教学中,我们是否经常或者近乎固执地把这样单一、模式化的解题方式灌输给学生呢?不可否认,你有,我有,他有,大家都有。】
突围:到底该怎么算?
师:哦!老师明白了!你们想的有一定道理,不过……
(画音刚落,有学生提出了不同想法。)
生2:老师,我认为不对。
师(故作惊讶表情):你是怎样想的呢?
生2:他们求出的并不是小正方形的周长。80是大正方形的周长,用80÷4=20(厘米),其实求出的是还是大正方形的边长,或者说是小正方形两条边长的和。
(看着大家疑惑的表情,该学生径自走上黑板,在图上做了小小的标注。)
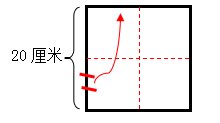
生3:哇!我一下看明白了,怎么就没想到呢?其实,我完全可以“描一描”小正方形的周长后,弄明白了再计算。
师:说的真好,先“描一描”小正方形的周长,再计算,这是多棒的办法呀!来,我们一起来“描一描”。
师:通过“描一描”,你想说些什么?
生4:求小正方形的周长,只要知道它的边长就好办了。
师:你能找到小正方形的边长吗?
生4:这就简单了,小正方形的边长是大正方形边长的一半,也就是20÷2=10(厘米)。
生(集体):我来算,我来算……
生5:老师,为了更好地理解,其实我还想到了一个好办法。
(同学们都目光所聚。)
生5:我想到了“切一切”的办法,就是从大正方形上拿一个小正方形下来,单独想一想它的周长该怎么算。
师:来,老师就按你的办法,拿一个出来,一起来看一看,你们认为怎么样?
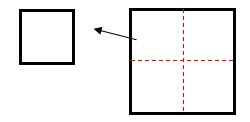
生6:这是一个好主意,这样“切一切”,拿一个下来,就更容易理解了,20÷2=10(厘米),求出小正方形的边长,10×4=40(厘米),多简单呀!
【旁白:错误并不可怕,可怕的是我们不愿意倾听孩子们错误背后的原生态思考。顺承着孩子们的思考误区,由“他们求出的不是小正方形的周长”这个点生发开来,通过磨、研、思、辩,以“描一描”、“切一切”为动态手段,直击求小正方形周长的要点,阐明要义,其中要旨,无需教师过多言说。】
升华:还可以怎样算?
正欲“鸣金收兵”之际……
生7:老师,我想到了不同的计算方法。
师:是吗?说来听听!
生7:我是这样算的: 20×2=40(厘米)。
师(故作好奇):还可以这样算?这又是怎么想的呢?
生7:根据前面的分析,我们知道了小正方形的边长是大正方形边长的一半, 所以,2条大正方形的边长就是4条小正方形的边长,所以就可以用20×2来计算小正方形的周长。(所有学生的解答中并未出现此种方法。)
师:大家听明白了吗?
生8:老师,我懂了,我还可以在图上来画一画,看的更清楚了。
师:好的,那请你来画一画。
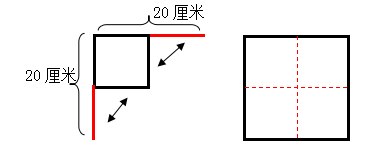
(掌声响起)
师:了不起!同学们从自己的错误中,灵活地寻找到正确的解决办法,相信在以后的学习中,一定会思考的更全面,感谢所有同学。
【旁白:恼人的错误,变得如此可亲可爱,对错误的探秘,成就了真相大白的无比精彩——思维的多元开放,方法的灵动巧妙。事实可见,孩子有洞察问题本质的能力,或许,我们在教学中,过多的牵引、喂食,方法的机械搬套,忽视学生内在的思维特质,才会导致解题中“尸横遍野”的场面。】
【启示】
所见即所得,直观化、表象化的学习行为,是小学阶段学生尤为明显的特征,这当然一方面受限于学生的年龄特征,同时较大程度地受制于教师的教学固守。在本案例中,导致错误的原因,是孩子们并不能完全“抽”出小正方形这一单一个体来进行针对性思考和解决。基于成人化的思维,我们教师理想地认为,理应是这样思考,却怎么就不能正确解决呢?正是过多的“理应”,固化了教师教学思维的同时,也羁绊了学生的思考进程。但是当探问到学生错误的原因之下,把学生见到的“表象”从直观意念中直接“剥离”开来,辅以前后承接上的具体的演化过程,孩子们的表现却能如此多姿多彩。源于此,贴近学生的思维而教,顺应孩子的天性而学,“理应”成为每一位数学老师孜孜以求的目标。
在这样的追求下,我们该何为?不妨以“三问”来做到时时自省。
一问:你把儿童当儿童了吗?
儿童只是儿童。但是,现如今功利化的教育价值导向,却让我们教师的眼里缺少了儿童韵味,这也导致我们面对的儿童不再是儿童。试问,你和现在的孩子能打成一片的吗?你的课堂中,还有小手林立,孩子们畅所欲言地表达着自己的想法吗?……不一而足。我想,更多的是,你为了完成自己预定的教学任务,面对孩子们的旁逸斜出,会无情地打断,硬扯着孩子们朝着自己预设方向航行。教师想的、做的、要求的,就是学生需要想的、做的,必须达到的。跳出教师自认为的“应该”,让孩子按照你认为的应该的标准解锁,儿童才能真正回归儿童。
二问:你了解孩子错误背后的原因吗?
孩子们学习中的错误,既是教学的资源,也是学习深入的路径。然,你面对孩子形形式式的错误,是否只有埋怨、只有感叹、只有无奈?你是否能主动地去了解孩子们错误背后的原因呢?其实,“笨有笨法,巧有巧劲。”孩子们在用自己的思考,竭力尝试问题得以解决。孩子们的错误,是他们学习中的问题所在,暴露出了思维中的盲点、断点、困惑点,我们不妨走近孩子,走进错误,或许,你能收获不一样的精彩。
三问:你了解孩子们的课堂需要吗?
每一个孩子都是独立的生命个体,他们有被认同、被尊重的需要。尤其在以孩子们为主体的课堂中,这种需要尤为强烈。可是,我们的课堂,给了孩子们多少自主权?孩子们的思维,是不是在我们强硬灌输和代替下,变得无趣,显得单一?我们仁慈地给孩子合作、交流、讨论、操作等活动,是不是形式大于内容?课堂上,孩子到底需要什么?或许,其答案是各人千面的,但我想,跳出说教的范畴,给学生以自主,顺承着孩子生长的意愿,在“助人自助”经历中,创造未知的精彩,生命之花才能绽放。
“千江有水千江月,万里无云万里云。”当我们放下过多的附加要求、控制和评价,从孩子的立场出发,去关注、关怀,孩子才有拔节生长的自然韵律,生命才能生动而自由起来。
发表于《小学数学教学案》2016年9期
 苏公网安备 32041202001123号
苏公网安备 32041202001123号 