缘起——老师,我怎么就错了呢?
“老师,我怎么就错了呢?”一位学生略带怯懦而又不甘的语气,指着自己练习卷上的一题问着我:
下图是一块梯形地的平面图,比例尺是1:20000,量出图上的上底是1厘米,下底是2厘米,高是3厘米。这块地的实际面积是多少平方米?
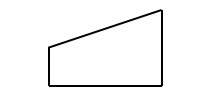
沿顺着琦的所指,卷面上的解法简洁而干脆:(1+2)×3÷2=4.5(平方厘米),4.5×20000=90000(平方厘米)=9(平方米)。
困局——这种解法也没错
显然,所得的结果与实际面积相差甚远,我批阅完全班的试卷,也正惊诧于此题错误之高,超乎我的想象,全班居然有14名同学的错误如出一辙,错误率达28%,我内心不禁暗暗问自己,学生不会根据求得的结果做出辨析,来判断正误吗?刚刚学习完《面积的变化》(苏教版六年级下册)一课,学生已经对面积的变化规律烂熟于胸:如果把一个图形按照n:1的比放大,放大后与放大前的面积比是n2:1,或者说如果把一个图形的边扩大n倍,面积就扩大n2倍。
课上,我先呈现出了正确的解法:
1×20000=20000(厘米)=200(米)
2×20000=40000(厘米)=400(米)
3×20000=60000(厘米)=600(米)
(200+400)×600÷2=180000(平方米)
我希冀让正确的同学们的思路,来“指正”那批学生的“误解”,出奇地顺畅而自然,学生也说的头头是道,全班同学都认为这种解法合情合理,都欣然接受。我畅快地舒了一口气,暗自庆幸。但是当我相机抛出琦的解法时,教室里炸开了锅,同学们一致认为,琦的做法也符合基本思考方向,在方法上是大同小异的,这种解法没有错。
学生们抛出了 “最充分”的理由:一种方法是根据比例尺,把这三条边各扩大20000倍,先求出梯形地的上底、下底和高的实际长度,然后来求实际面积;琦的做法是先求出图上面积,然后把图上面积扩大20000倍,异曲同工呀,遗憾的是为什么结果怎么就不同了呢?僵局就此形成,矛盾的结果,一下把学生带入了思维的漩涡,无力自拔。
我不禁暗暗地责怪起自己来,说实话,此种类型的问题,在以前有多次接触和练习,大多是给出图上的长方形、正方形或圆形的平面图以及对应的比例尺,计算实际面积,相对比较简单,我做了反复强调和硬性规定,先要求出实际长度,再根据实际长度求实际面积,固定的解法,已成模式,学生求解也是得心应手。但是为什么要先求出实际长度,再求实际面积,此中理由,偶有涉及,因为学习《面积的变化》一课之后,我自以为是地认为学生应该能明了其中原委。
重构——基于学生思维的再认识
面对这样的“困局”,我只有寻求突围之径,于是乎,我重设了今天的教学路径,开始了与学生的“重新对话”,以期突破面临的思维“桎梏”。
一、基础铺垫
出示:
1、一个长方形长是3厘米,宽是2厘米,把它的长和宽扩大2倍,面积扩大( )倍。
2、把一个圆的半径扩大3倍,面积扩大( )倍。
学生都能顺利解答,快速而顺畅地得到结论:长方形的面积扩大4倍,圆的面积扩大9倍。
二、呼应提升
1、把一个边长是6厘米的正方形的边长扩大200倍,面积扩大多少倍?
学生依然能毫无梗阻地得出面积扩大40000倍。
2、一块三角形果园,按1:300的比画在图纸上,底是4厘米,高是3厘米。实际面积是图上面积的多少倍?
(这一题,省略掉了实际面积的探求,直接顺应着前面的问题,进行同类型问题的解决,学生明显有卡顿的现象。)
师:同学们,你们觉得结果该是多少呢?
生1:300倍。
生2:不对,应该是90000倍。
生3:我觉得应该先来算一算图上面积和实际面积,才能得到结果。
师:那我们不算能得到结果吗?
生4(抢着说):不用算!
师(疑问的表情):说说你的想法。
生4:这题,其实和前面的题目完全是同类型的,‘按1:300的比画在图纸上’,意思就是说实际长度是图上长度的300倍,不信,我可以换一种意思说:把一个底是4厘米,高是3厘米的三角形,扩大300倍,面积扩大多少倍?(投影相机出示题目)
(听着这位学生的分析,在座的同学眼睛中有原来略带迷茫的表情转而变为清澄,由此,阻塞的思维通道逐渐畅通。)
师:哪到底扩大多少倍呢?
生(齐):90000倍。
师:为什么呢?相信大家已经在完全理解这题的意思后,与我们早前学习的规律对应起来了。不过,下面,我还是想听同学们通过计算验证下。
生:我先算出图上的面积,4×3÷2=6平方厘米;再计算实际的面积,先要把底和高扩大300倍,求出实际长度,(4×300)×(3×300)÷2=540000平方厘米,540000÷6=90000,确实是90000倍。
师:如果把一个图形的边扩大n倍,面积就扩大n2倍。我们再次进行了验证。
三、迁移拓展
师:那我们再回到那道梯形问题上来,大家还想说些什么?
生:求梯形地的实际面积,我们可以根据比例尺求出上底、下底和高的实际长度,再就实际面积。
师:哪大家想对琦同学的解法说些什么呢?
生:琦,你的方法不完善,按照我们的验证,根据面积的变化规律,求出了图上面积,应该把图上面积扩大200002倍才是梯形菜地的面积。所以你可以这样算:(1+2)×3÷2=4.5(平方厘米),4.5×20000×20000=1800000000(平方厘米)=180000(平方米)。
……
计算“这块梯形地的面积”,本是规律的顺承运用,但是,从平常基本的练习路径来看,较多的是涉及的“把一个基本图形的边长扩大n倍,面积扩大多少倍?”而且,n一般是在10以内的自然数,此种类型的题目,规律的简单套用,学生解决毫无阻梗,但当面对“一块三角形果园,按1:300的比画在图纸上,底是4厘米,高是3厘米。实际面积是图上面积的多少倍?”之例,学生接触不多,规律内化不够,甚至可以说是从未触及,有“琦”之问也在常理之中。“求出图上面积,再根据比例尺求出实际面积”,实际上是忽略的了规律自身的内核,本质上是对规律内在的联系不甚通晓,也可以说是思维纽带的断裂。
启示——重新演绎故事里的“事”
学生已然明白个中缘由,然,于我而言,内心却有一种“痛则不通”的挫败感,我期冀找寻到“通则不痛”的“秘制良方”。细细思忖之下,还是缺少教与学之间的一份应然通融,未能促成学生凌空而悬的思维真正“着陆”。
突破“我要的是葫芦”的狭隘短见。明明是学生在学习中会遇到的“盲点”,思考中遇阻的“断层”,教师在教学中却视而不见,为追求结果不关注细节,正是我们教师平常的教学活动中频繁发生的“案例”,以己度人,却忽略了学生是需要我们关照下拔节成长的“小精灵”。“先求出图上面积,再把图上面积扩大20000倍就可以求出梯形地的实际面积”,印证了病症所在。边线之变之于面积之变,虽有规律护航,但是,规律的形成,需要一个实实在在的“探理”过程,理已在,用却乱,归根结底,是理没能导思,未能促用。这也警示我们每一位数学教育工作者,在教学中,切勿想当然,求速成,切忌高跨越、短视域,更不宜用结果代替过程,而应该在充分的预设中,正视学生的困难,做到在预见中遇见,让学生经历自己的研究和探索过程,通过必要的变式,尝试“磨研思辨”的全方位验证,把知识前后贯通起来,把问题的解决当作锤炼思维的提升过程,演绎出新版的“我要的是葫芦”的动人故事。
无惧“亡羊补牢”救赎。俗话说“亡羊补牢,未为晚矣!”相信,每一位教学工作者,都曾经面对过教学中的种种偏差。把繁难的知识教的通俗易懂,这是教学的水平,但不可否认的是,任何一位教师总会在自己“固有”思维的认识下,教学偏离了预期的航向,收到了适得其反的效果,或者说学生学而未懂,抑或懂而不善用,这并不可怕,教师需要做的是及时反思自己的教学行为,调整自身的教学策略,深入透彻地洞悉知识的生发点和联结点,同时跟进学生思维动向,了解他们的学习起点,切准学生的困惑、疑难,在学生的思维盲点、断层之处,相机架起贯通的桥梁,教与学就不会脱节,练与用也能趋于相承有度。智者无惧,“亡羊补牢”未尝不是一个教师的励志故事。
教师,需要用审慎的态度,去直面我们的孩子;教学,需要理性地走进课堂,紧随孩子左右,切准学生思维的韵律前行。
发表于《新教师》杂志2016年6期
 苏公网安备 32041202001123号
苏公网安备 32041202001123号 